Notice
반응형
Recent Posts
Recent Comments
Link
250x250
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 이클립스
- js
- Stack
- jsp
- java
- 문제풀이
- SQL
- googleChart
- script
- BREW
- 정처산기
- set
- 에라토스테네스의 체
- 백준
- html
- IntelliJ
- Eclipse
- react
- TSX
- input
- 자료구조
- 수학
- 응용SW
- Oracle
- node
- 책추천
- Algorithms
- npm
- deque
- HashMap
Archives
- Today
- Total
개발하자
[백준][Java] 11050번 이항 계수 1 본문
728x90
안녕하세요 :)
적어도 하루 1개 이상 알고리즘 문제를 해결하려 노력하고 있습니다.
혼자 해결 가능한 문제도 있고, 어려웠던 문제도 있던 차라 복습하고자 글을 써 내려갑니다.
백준 11050 이항 계수 1
오늘은 수학 시간에 배운 이항계수 개념을 코드로 구현해보는 문제였습니다.
문제 설명과 함께 이항계수가 뭔지도 간단히 정리해 보았습니다.
📘 문제

💡 해결 방법
이 문제는 수학에서 이항계수(Binomial Coefficient) 개념을 활용해 푸는 문제입니다.
공식은 다음과 같습니다.
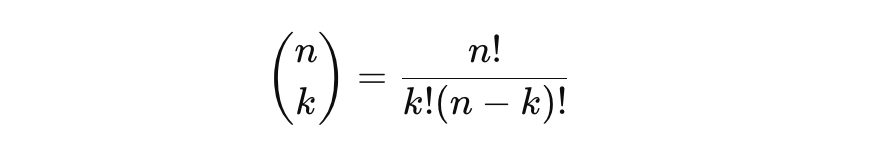
즉, n개의 원소 중에서 k개를 선택하는 경우의 수를 계산하는 것이죠.
중복 없이 순서를 고려하지 않고 선택하는 조합(combination)을 의미합니다.

하지만 그대로 팩토리얼을 계산하면 큰 수가 나올 수 있기 때문에,
계산을 최적화해서 하나씩 곱하고 나누는 방식으로 구현할 수 있습니다.
✅ 풀이 및 설명 (설명은 더보기 클릭)
더보기
- 입력으로 n, k 값을 받습니다.
- 이항계수를 구하는 binomialCoefficient() 메서드를 별도로 만들어 계산합니다.
- k > n - k일 경우, k 값을 줄여서 반복 횟수를 줄여 최적화합니다.
- (n - i)를 곱하고, 동시에 (i + 1)로 나누는 방식으로 이항계수를 구합니다.
- 팩토리얼을 직접 계산하지 않고 계산 중간마다 나눠주기 때문에 오버플로우 위험이 적고 성능도 좋습니다.
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] input = br.readLine().split(" ");
int n = Integer.parseInt(input[0]);
int k = Integer.parseInt(input[1]);
System.out.print(binomialCoefficient(n, k));
br.close();
}
private static long binomialCoefficient(int n, int k) {
if (k > n - k) {
k = n - k; // k가 더 크면 n - k로 바꿔서 계산 최적화
}
long result = 1;
// (n - k + 1)부터 n까지 곱하고 k!로 나누는 방식으로 계산
for (int i = 0; i < k; i++) {
result *= (n - i);
result /= (i + 1); // 나누면서 계산하기
}
return result;
}
}
이항계수는 수학적인 개념이지만 알고리즘 문제에서도 자주 등장하는 개념입니다.
특히 조합이나 확률 문제, DP 등에서 많이 활용되므로 개념과 구현법을 익혀두면 좋아요.
공부하면서 유용했던 부분 메모 겸 공유하고자 끄적입니다.
고쳐야 하는 부분 있다면 댓글 남겨주시면 수정하겠습니다.
행복한 하루 보내세요 (❁´◡`❁)
728x90
반응형
'Algorithms > Baekjoon' 카테고리의 다른 글
| [백준][Java] 25192번 인사성 밝은 곰곰이 (0) | 2025.04.29 |
|---|---|
| [백준][Java] 1037번 약수 (0) | 2025.04.29 |
| [백준][Java] 24723번 녹색거탑 (2) | 2025.04.28 |
| [백준][Java] 15439번 베라의 패션 (2) | 2025.04.28 |
| [백준][Java] 24511번 queuestack (5) | 2025.04.26 |




