Notice
반응형
Recent Posts
Recent Comments
Link
250x250
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
Tags
- HashMap
- 수학
- script
- 문제풀이
- BREW
- 자료구조
- jsp
- Algorithms
- deque
- 정처산기
- googleChart
- 응용SW
- SQL
- set
- java
- Eclipse
- 에라토스테네스의 체
- react
- npm
- Oracle
- 백준
- node
- html
- js
- 이클립스
- Stack
- input
- 책추천
- IntelliJ
- TSX
Archives
- Today
- Total
개발하자
[백준][Java] 1269번 대칭 차집합 본문
728x90
안녕하세요 :)
적어도 하루 1개 이상 알고리즘 문제를 해결하려 노력하고 있습니다.
혼자 해결 가능한 문제도 있고, 어려웠던 문제도 있던 차라 복습하고자 글을 써 내려갑니다.
백준 1269 대칭 차집합
이번 문제는 집합(Set) 개념을 이해하고 있다면 어렵지 않게 풀 수 있는 문제입니다.
대칭 차집합이 무엇인지 알고, HashSet을 이용해 효율적으로 푸는 연습에 적합한 문제였어요.
📘 문제
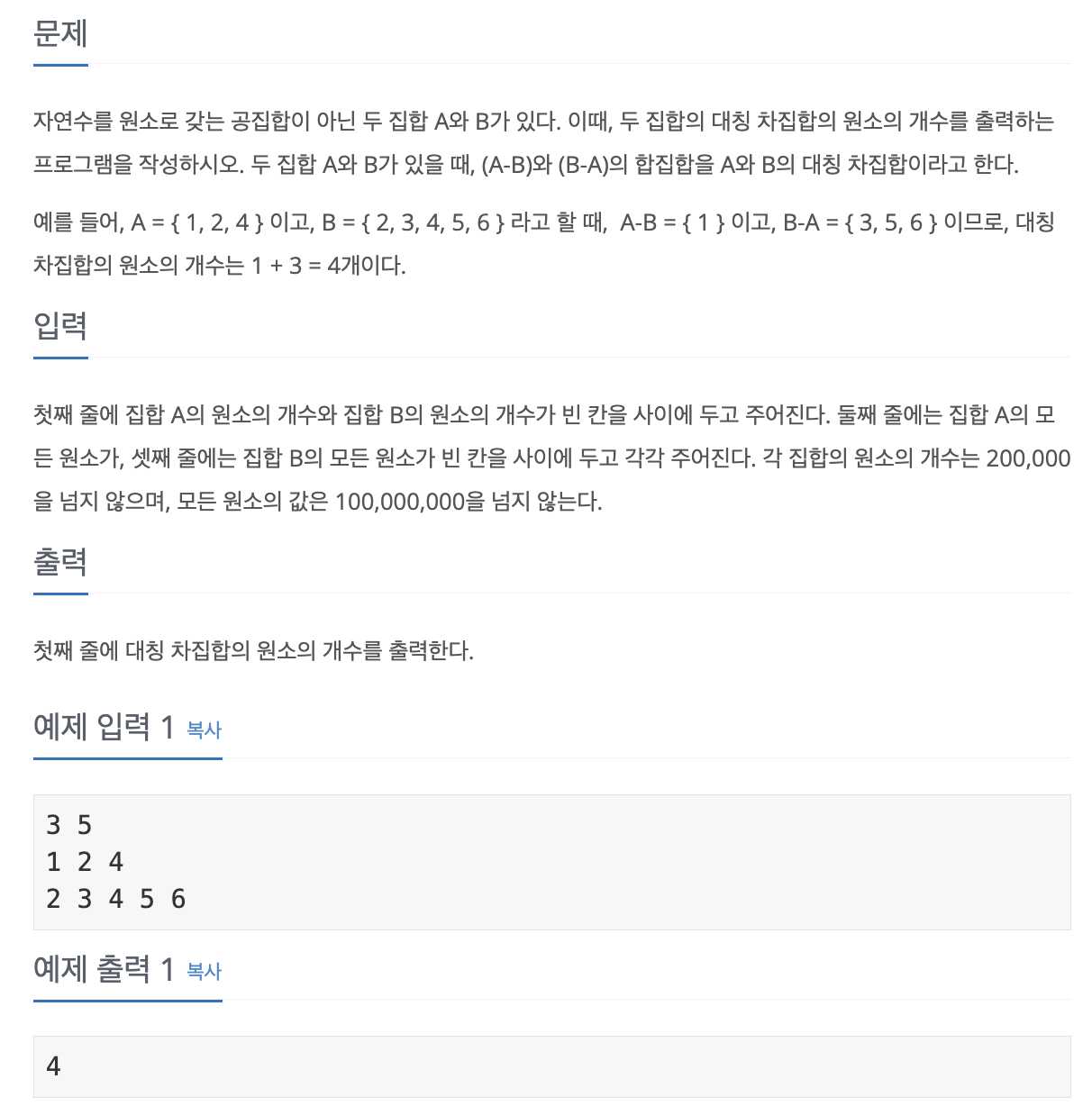
💡 해결 방법
대칭 차집합은 두 집합에서 서로 겹치지 않는 원소들의 합집합입니다.
예를 들어, A ∆ B = (A - B) ∪ (B - A)
즉, 겹치는 요소를 제외한 원소의 개수를 출력하면 됩니다.
✅ 풀이 및 설명 (설명은 더보기 클릭)
더보기
- 먼저 A 집합의 원소들을 HashSet에 저장합니다.
- B 집합을 순회하며 A 집합에 포함되어 있는지 확인합니다.
- 포함되어 있다면 **겹치는 원소의 개수(match)**를 증가시킵니다.
- 대칭 차집합의 개수는 (A의 전체 개수 - match) + (B의 전체 개수 - match)입니다.
import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// A와 B의 원소 개수 입력
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
// A 집합 원소 저장
Set<Integer> setA = new HashSet<>();
st = new StringTokenizer(br.readLine());
for (int i = 0; i < n; i++) {
setA.add(Integer.parseInt(st.nextToken()));
}
// B 집합과 비교하면서 겹치는 원소 개수(match) 세기
st = new StringTokenizer(br.readLine());
int match = 0;
for (int i = 0; i < m; i++) {
int b = Integer.parseInt(st.nextToken());
if (setA.contains(b)) {
match++;
}
}
// 대칭 차집합 = (A - 공통) + (B - 공통)
System.out.println((n - match) + (m - match));
br.close();
}
}
대칭 차집합의 정의를 이해하면 수학적으로 바로 식을 세울 수 있어 좋았습니다.
시간 제한이 있는 문제에서는 HashSet처럼 검색이 빠른 자료구조를 사용하는게 정말 중요하다는걸 다시 느꼈어요.
자바의 HashSet.contains()는 평균 O(1)이라 교집합 체크에 매우 유용합니다.
공부하면서 유용했던 부분 메모 겸 공유하고자 끄적입니다.
고쳐야 하는 부분 있다면 댓글 남겨주시면 수정하겠습니다.
행복한 하루 보내세요 (❁´◡`❁)
728x90
반응형
'Algorithms > Baekjoon' 카테고리의 다른 글
| [백준][Java] 1934번 최소공배수 (6) | 2025.04.20 |
|---|---|
| [백준][Java] 11478번 서로 다른 부분 문자열의 개수 (0) | 2025.04.20 |
| [백준][Java] 1764번 듣보잡 (0) | 2025.04.20 |
| [백준][Java] 10816번 숫자 카드 2 (1) | 2025.04.20 |
| [백준][Java] 2480번 주사위 세개 (0) | 2025.04.20 |




